#include <FSimpleTVInpaintingSpace.hpp>
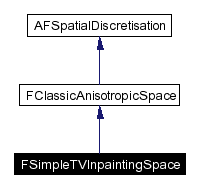
Inheritance diagram for FSimpleTVInpaintingSpace:


Variational Image Restoration
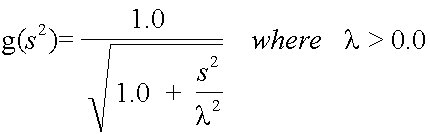
Variational Convex Potential
Purpose: Variational Restoration uses a reaction diffusion approach,
the reaction term ensures that the evolution is always near the original image.
It is more robust against strong noise that classic diffusion, but do not enhance edges.
ut= div( g(|grad(u)|^2) grad(u)) + beta*(f-u)
g(s2)= 1.0/sqrt(1.0+ s2/contrast*contrast);
Variational Restoration can be used in cascade to do a pyramidal restoration.
Paper: "Mathematical Models for Local Deterministic Inpaintings", Tony Chan & J. Shen,
Report 2000, UCLA, USA.
"Efficient Image Segmentation Using Partial Differential Equations and Morphology.",
Joachim Weickert, Technical Report 3/2000, Computer Science Series,
DIKU, University of Copenhagen, Denmark.
"Evaluation of Diffusion Schemes for Multi-scale Watershed Segmentation.", Erik B. Dam,
Thesis 2000, Computer Science, University of Copenhagen.
"Edge-Preseving Noise Removal, Part I: Second-Order Anisotropic Diffusion.",
Seongjai Kim, Technical Report 2001-09, University of Kentucky.
"MinBAD: The Minimum-Biased Anisotropic Diffusion for Noise Removal.",
Seongjai Kim & all, Technical Report 2002-06, University of Kentucky.
"PDE-based image restoration,II: Numerical schemes and color image denoising.",
Seongjai Kim & all, Technical Report 2003-08, University of Kentucky.
"Image Analysis & Edge-Preseving Noise Removal.",
Seongjai Kim, Presentation 2003, University of Kentucky.
@ Copyrights: Bernard De Cuyper 2004, Eggs & Pictures. MIT/Open BSD copyright model.
Public Methods | |
| FSimpleTVInpaintingSpace (double sigma=2.0, double acontrast=1.0, double abeta=0.0, int diffusivity=0, int gradType=0) | |
| virtual | ~FSimpleTVInpaintingSpace () |
| virtual void | setI0 (FImage *u0) |
| virtual FImage * | getI0 () |
| virtual void | setInpaintingDomain (AnImage *area) |
| virtual AnImage * | getInpaintingDomain () |
| virtual void | setExtensionDomain (AnImage *area) |
| virtual AnImage * | getExtensionDomain () |
| virtual void | setTauRight (float t) |
| virtual float | getTauRight () |
| virtual AFSymMatrix * | getA (float tau, FImage *uk, AFSymMatrix *A=0) |
| virtual FloatVector * | getB (FImage *ik, FloatVector *uk=0) |
| virtual AFSymMatrix * | getRowA (float tau, FImage *uk, int row, AFSymMatrix *A1=0) |
| virtual AFSymMatrix * | getColA (float tau, FImage *uk, int col, AFSymMatrix *A2=0) |
| virtual FloatVector * | getRowB (FImage *ik, int row, FloatVector *uk=0) |
| virtual FloatVector * | getColB (FImage *ik, int col, FloatVector *uk=0) |
Protected Methods | |
| virtual FImage * | gValues (FImage *src, FImage *dest=0) |
Protected Attributes | |
| float | tauRight |
| float | beta |
| float | betaCorrection |
| FImage * | f |
| AnImage * | inpaintingDomain |
| AnImage * | extensionDomain |
 |
