#include <AFSplittedRestorationLS.hpp>
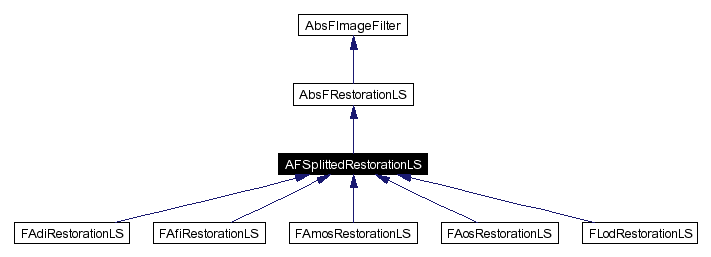
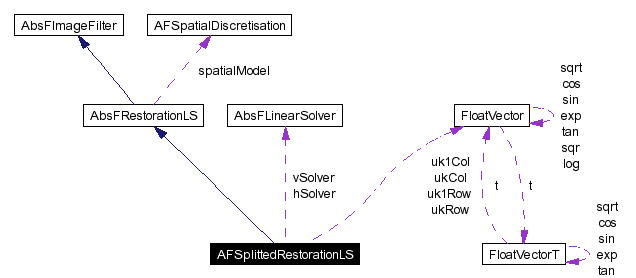
Inheritance diagram for AFSplittedRestorationLS:

Purpose: Fast Computation of Splitted 2D Solvers
One way is using the realtime Thomas LU model which provides constant time results
in the semi-Implicit case:
(I - tau * A) * uNew= uOld
Splitted solvers are designed for large image restoration, O(N) in time and space!!!
Implicit solvers like ADI are also possible, more accurate but under certain conditions of timesteps.
Implicit solvers are not absolutely stable, like semi-implicit one.
ADI case: Splitted implicit solver using tridiagonals solvers (in case of five point stencils)
(I - tau/2 * Ax) * u$= [(I + tau/2 * Ay)] * uOld // X-sweep
(I - tau/2 * Ay) * u= [(I + tau/2 * Ax)] * u$ // Y-sweep
Papers: "Recursivity and PDE's in image processing",
L. Alvarez, R. Deriche and F Santana, Spain 1998.
"Efficient and Reliable Schemes for Nonlinear Diffusion Filtering",
Joachim. Weickert & all, IEEE transactions on Image Processing, vol7, n3, March 1998.
"Operator Splitting Techniques For Unsteady Navier Stokes Equations",
Seongjai Kim, University of Kentucky, 2000.
"Fractional Time Stepping Methods for Unsteady Flow Problems",
Seongjai Kim & Jim Douglas, University of Kentucky, 2000.
"Recursivity and PDE's in image processing",
L. Alvarez, R. Deriche and F Santana, Spain 1998.
"Numerical Receipes in C: Diffusion Equation in Multidimensions.", p666,
William H. Press & all, Cambridge University Press, 1988.
"Numerical Receipes in C: 17.6, Operator Splitting Methods and ADI.", p681-688,
William H. Press & all, Cambridge University Press, 1988.
Fast ADI_II (Kim 2000) is a DPR-ADI with splitting correction to "mimic the Cranck-Nicolson without error"
Public Methods | |
| AFSplittedRestorationLS (int outerIter, int innerIter, double t, AFSpatialDiscretisation *smodel, bool normalized=true, bool nonLinearFlag=true) | |
| AFSplittedRestorationLS (int model, int outerIter, int innerIter, double t, AFSpatialDiscretisation *smodel, bool normalized=true, bool nonLinearFlag=true) | |
| virtual | ~AFSplittedRestorationLS () |
| virtual void | setHSolver (int model) |
| virtual void | setVSolver (int model) |
| virtual FImage * | filter (FImage *src, FImage *dest=0) |
| Local full image filtering. | |
| virtual void | report (FILE *file) |
Protected Attributes | |
| int | solverType |
| AbsFLinearSolver * | hSolver |
| AbsFLinearSolver * | vSolver |
| FloatVector * | ukRow |
| FloatVector * | uk1Row |
| FloatVector * | ukCol |
| FloatVector * | uk1Col |
|
||||||||||||
|
Local full image filtering.
Reimplemented from AbsFRestorationLS. |
 |
